Teorema del factor, división sintética y regla de signos de Descartes.

a) Teorema del factor

Establece que los ceros de polinomios corresponden a factores.

c es un cero de P si y solo si x- c es un factor de P(x).

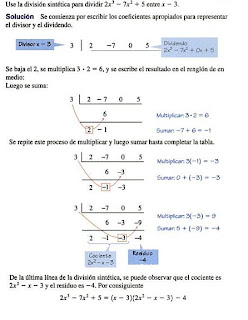
b) Division Sintetica

Es un metodo rapìdo de dividir polinomios; se puede usar cuando el divisor esta en forma de x - c. En la division sintetica se escriben solo las partes esenciales de la division larga.

En el ejemplo siguiente se muestra la division sintetica efectuada.

c) Regla de signos de Descartes

Sea p(x) un polinomio con coeficientes reales tal que p(0) sea diferente de 0.Entonces:
1.- El numero de raices reales positivas de p(x) es igual al numero de variaciones en el signo de p(x) o es menor que ese numero por un entero par.

2.- El numero de raices reales negativas de p(x) es igual al numero de variaciones en el signo de p(-x) o es menor que ese numero por un entero par.
.

Bibliografia:

 - Precalculo: Matematicas para el calculo de James Stewart,Lothar Redlin
- Algebra y trigonometria con geometria analitica de Arthur Goodman,Lewis Hirsch

Teorema fundamental del álgebra, método de Ruffini y teorema del Resto

a) Teorema fundamental del álgebra

En el sistema de numeros complejos un polinomio de n-esimo tiene exactamente n ceros y por lo tanto, se puede factorizar exactamente n factores lineales. Este hecho es una consecuencia del teorema fundamental del álgebra, el cual fue probado por el matematico alemán C.F. Gauss en 1799.

Este teorema es la base para gran parte del trabajo de factorizar polinomios y resolver ecuaciones polinomiales.

b) Método de Ruffini

El algoritmo de Ruffini es un método para hallar las soluciones de ecuaciones de cualquier orden, a condición de que sus soluciones sean enteras. Para soluciones fraccionarias, este método resulta basntante difícil.
Por otra parte, este algoritmo también sirve para facorizar ecuaciones o expresiones matemáticas. La mejor forma de explicar el método es a través de uin ejemplo.

c) Teorema del Resto

Dado un polinomio P(x), diremos que a es una raiz de P(x) si P(a)=0.
Consideremos P(x) un polinomio de coeficientes reales y sea a un numero real cualquiera. Si dividimos P(x) entre x - a obtendremos un polinomio cociente C(x) y un Rrsto R.
Por tanto, tenemos:

P(x) = C(x) . (x - a) + R

Si calculamos P(a) en la expresion anterior, tenemos:

P(a) = C(a) . (a - a) + R = 0 + R =R

Teorema del Resto: El resto de dividir un polinomio P(x) entre x - a es P(a).

Consideremos un polinomio P(x) con coeficientes enteros y a pertenece a Z una raiz de P(x), entonces a divide al termino independiente de P(x).
Los candidatos a raiz entera de un polinomio con coeficientes enteros son los divisores de su térmi9no independiente.

Bibliografia:
 - Precalculo: Matematicas para el Calculo de James Stewart,Lothar Redlin
- La matematica es facil: Manual de matematicas basica para gente de letras de José Manuel Casteleiro Villalba
- Matematicas 4o ESO Opcion A de Germán González Pérez